DeepSeek API: A Guide With Examples and Cost Calculations

Notice! The promotion has been recently updated, changing from $1 for the first month to $9.9 for 12 months, making it even cheaper.

Notice! The promotion has been recently updated, changing from $1 for the first month to $9.9 for 12 months, making it even cheaper.

In this tutorial, I will show you how to set up and use the DeepSeek API so you can integrate it into your projects. You'll learn:

• Available models: deepseek-chat (V3) & deepseek-reasoner (R1), and how to access them via API.
• Key parameters: How to control the model’s output and manage pricing.
• Chain-of-thought pricing: How DeepSeek calculates costs based on reasoning complexity.
• Context caching: A smart way to reduce costs when using DeepSeek.

By the end, you’ll know how to use DeepSeek while keeping costs low. Let’s get started! 

DeepSeek Models

DeepSeek provides two main models that you can use through an API:

1. DeepSeek-V3 (deepseek-chat): A generalist model trained on a massive amount of text (15 trillion tokens).
2. DeepSeek-R1 (deepseek-reasoner): A model designed for advanced reasoning, math, and coding tasks.

How to Access DeepSeek R1 and V3 via API

To access the DeepSeek models via API:

1. Get an API key: Sign up on the DeepSeek API platform and generate your key.
2. Use the OpenAI SDK (Software Development Kit): Set up your code to connect to the DeepSeek API using OpenAI’s SDK with the correct settings. An SDK is a collection of tools, libraries, documentation, and code samples that helps you build applications for a specific platform, framework, or API. An API SDK (like the OpenAI SDK) provides ready-to-use functions to make API calls easier, so developers don’t have to write everything from scratch.

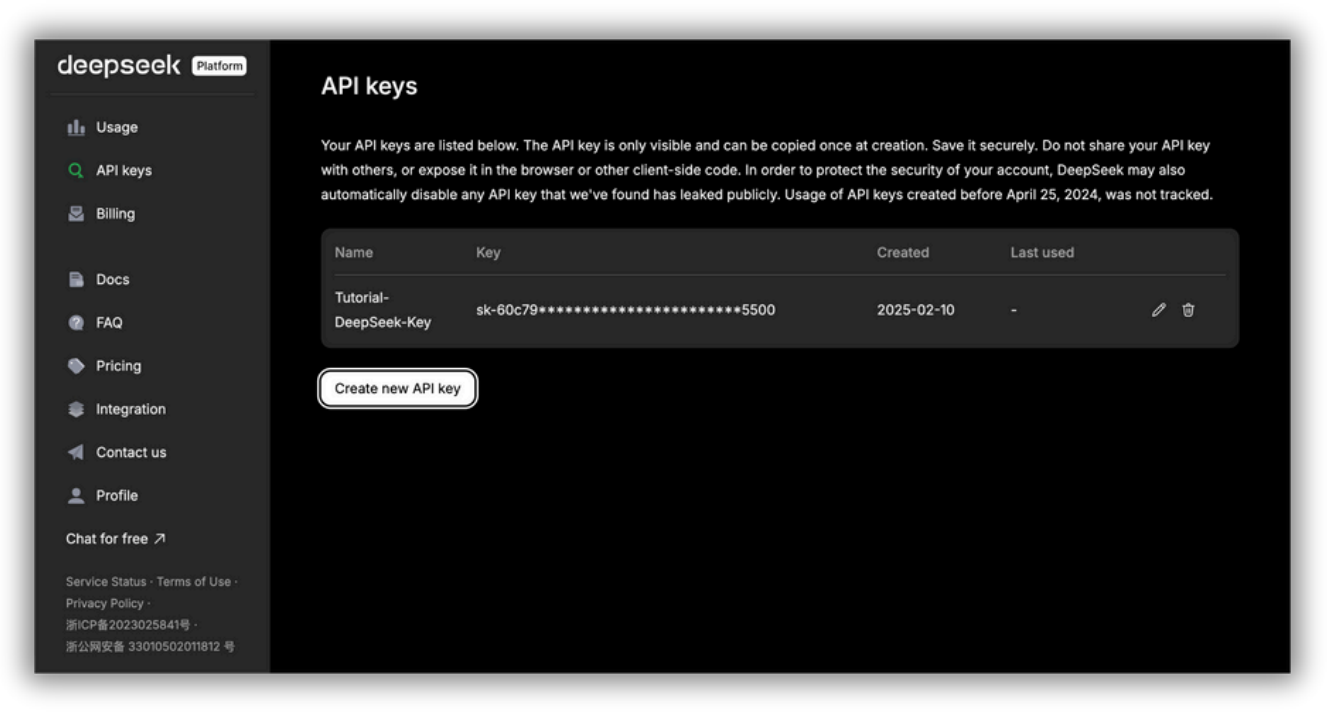
DeepSeek API platform API key management page. Here you can generate and manage your API keys for accessing DeepSeek's AI services. The API key is only visible at creation and must be securely stored; sharing it publicly can lead to security risks.

To use DeepSeek-V3 you will need to set model='deepseek-chat' and to use DeepSeek-R1 you will need to set model='deepseek-reasoner'.

Here is how you can use the OpenAI SDK to access the DeepSeek API:

from openai import OpenAI
client = OpenAI(api_key="<DeepSeek API Key>", base_url="https://api.deepseek.com")
response = client.chat.completions.create(
    model="deepseek-chat",
    messages=[
        {"role": "system", "content": "You are a helpful assistant"},
        {"role": "user", "content": "Hello"},
    ],
    stream=False
)
print(response.choices[0].message.content)

Let’s have a closer look at what this piece of code does. 

The code's goal is to send a chat message to the DeepSeek model and print the model's response.

First, from openai import OpenAI imports the OpenAI class from the openai library. 

Then, client = OpenAI(...) creates an OpenAI client object. This client is your connection to the DeepSeek API. It configures the client with your API key (authentication) and specifies the DeepSeek API's base URL. 

Important: Replace <DeepSeek API Key> with your actual DeepSeek API key!

The response is the part that sends your chat message to the DeepSeek model and gets the response. client.chat.completions.create(...)  is calling the DeepSeek API to get a response from the model.

Let’s look at messages=[...], which is the part that defines the conversation history:

• System message: {"role": "system", "content": "You are a helpful assistant"}: This sets the model’s behavior, telling it to act like a helpful assistant.
• User message: {"role": "user", "content": "Hello"}: This is the actual user input (your prompt) that the AI should respond to ("Hello").

Note that in this example we are using DeepSeek-V3 as we have set model='deepseek-chat’ but remember that you can use DeepSeek-R1 by setting model='deepseek-reasoner'.

The stream=False part means "Give me the whole answer at once." Basically, when you set stream=False, the model waits until it has generated the entire response before sending it back. Use this if you want to display or analyze the complete response at once.

However, you might have to wait a bit for long responses before receiving the output. If you set stream=True, the model shows words (well, tokens) as they are generated, so you see the response in real time instead of waiting for the full answer.

Finally, print(response.choices.message.content) extracts the model's response from the response object and prints it to your console. The response object contains a lot of information, but you're primarily interested in the model's message. The API can sometimes return multiple possible answers (choices). This selects the first one.

At the time of publishing this article, DeepSeek has paused adding new funds to API accounts because their servers are running low on resources. That means that you can’t add more money to your API balance right now. If you already have funds, you can still use the API as normal. DeepSeek will likely resume recharges once they have more server capacity, so keep an eye out for updates!

Managing Parameters to Control Output and Pricing

The DeepSeek team claims their models are cheaper than the competition. But you still need to use it wisely to keep costs low and get the best performance. Here are the key things to know and take into consideration when using DeepSeek’s models to control the output and pricing.

Choosing the right model

Each DeepSeek model is designed for different tasks. Picking the right one can help you balance cost and performance based on your needs. Here's a quick comparison:

• deepseek-chat (V3):Cheaper, good for general chat and conversations.
• deepseek-reasoner (R1) →More expensive, but great for complex reasoning and advanced tasks.

Token costs

Tokens are the smallest unit of text that the model processes, which can be a word, number, or even a punctuation mark. The number of tokens used depends on the language and the way the model processes text.

Here’s a general comparison of how characters convert to tokens:

• 1 English character ≈ 0.3 tokens (A 100-character sentence would be around 30 tokens).
• 1 Chinese character ≈ 0.6 tokens (Since Chinese characters convey more meaning per character).

To get an accurate estimate, it's best to check the usage details after running your request. If you understand how tokens are counted, you can better manage costs and optimize performance when using DeepSeek’s models.

Here are the prices per 1 million tokens for each of the DeepSeek models (note: these were the prices at the time of publishing this article—check the most recent costs here):

Model	Context length	Max cot tokens	Max output tokens	1m tokens input price (cache hit)	1m tokens input price (cache miss)	1m tokens output price
deepseek-chat	64k	-	8k	$0.07	$0.27	$1.10
deepseek-reasoner	64k	32k	8k	$0.14	$0.55	$2.19

As mentioned before, DeepSeek offers two models, deepseek-chat and deepseek-reasoner. But each comes with different strengths and costs. Knowing how they process information and charge for tokens can help you use them more efficiently and keep costs under control.

Both models can handle up to 64,000 tokens in a conversation, meaning they remember more context for better, more relevant responses. However, they work differently.

Deepseek-chat is designed for general conversations and doesn't use advanced reasoning. Deepseek-reasoner, on the other hand, allows up to 32,000 tokens for step-by-step thinking (chain-of-thought reasoning—more on this in a bit) before giving a final answer. This makes it great for solving complex problems but also increases the number of tokens used, and this means higher costs.

When it comes to response length, both models can generate up to 8,000 tokens per reply. This limit helps prevent responses from getting too long and expensive.

Looking at pricing, deepseek-chat is the more budget-friendly option. If the input is cached (meaning it has been used before), it costs $0.07 per million tokens. For new input, the price goes up to $0.27 per million tokens, and the output costs $1.10 per million tokens.

Deepseek-reasoner is more expensive because it provides deeper reasoning. Cached input costs $0.14 per million tokens, while new input costs $0.55 per million tokens. Its output is also pricier at $2.19 per million tokens, reflecting the complexity of the responses it generates.

So, which model should you use? 

If you need simple chat responses or quick answers, deepseek-chat is the better choice because it’s cheaper. But if you need detailed reasoning or complex problem-solving, deepseek-reasoner is more powerful—though it costs more.

To save money, you can also use caching. When the model recognizes input it has seen before, it charges a lower rate. This is really useful for repeated queries or multi-turn conversations.

DeepSeek models are competitively priced, but token usage can add up quickly. The best way to manage costs is to keep prompts short, use caching when possible, and choose the right model for the job.

The temperature parameter

The temperature parameter controls how random or predictable the model’s responses are. By default, in DeepSeek it is set to 1.0, meaning responses are balanced between being creative and deterministic. However, you can adjust this setting depending on your specific needs.

DeepSeek provides the following recommendations for different use cases:

Use Case	Recommended Temperature
Coding / Math	0.0 (Deterministic, precise)
Data Cleaning / Data Analysis	1.0 (Balanced responses)
General Conversation	1.3 (More variety in responses)
Translation	1.3 (Allows flexibility in wording)
Creative Writing / Poetry	1.5 (Encourages diverse, imaginative output)

A low temperature (close to 0.0) makes the model more predictable and precise. This is great for tasks requiring accurate answers, like coding, math, and structured data analysis.

A higher temperature (above 1.0) makes the model more creative and varied, suitable for storytelling, poetry, and translations where flexibility is needed.

For general conversations, a temperature around 1.3 helps produce natural and engaging dialogue without being too repetitive or overly random.

While the temperature setting itself does not directly affect costs, it can indirectly increase the number of output tokens:

• Higher temperatures can result in longer and more varied responses, which means more tokens are generated—leading to higher costs.
• Lower temperatures often result in shorter, more direct answers, which reduces token usage and keeps costs lower.

Response format

When interacting with DeepSeek’s API, you can control the format of the responses by specifying the response_format parameter. This is especially useful when working with structured data, as it helps ensure consistency and readability in the model’s output.

To receive responses in JSON format, set:

response_format={'type': 'json_object'}

JSON format is commonly used in applications that require structured, machine-readable responses, such as data extraction, automation, and API integrations.

Even though JSON formatting does not directly impact pricing, it can indirectly reduce costs in certain cases.

• More concise responses: Since JSON responses follow a structured format, they tend to be more compact, potentially using fewer tokens than free-text responses.
• Improved Accuracy: If you explicitly request structured output, you minimize the risk of long, unnecessary explanations, helping to control token usage.

Understanding Chain-of-Thought (CoT) and Its Costs

CoT is the reasoning process that DeepSeek-R1 goes through before giving a final answer. This means the model explains its thought process step by step before reaching a conclusion.

Every token used in the CoT reasoning and the final answer is charged at $2.19 per million tokens, as it is part of the output. It is a bit of a trade-off; more CoT tokens = more cost but also better accuracy in complex tasks.

What can you do to control costs while using CoT?

• Use clear prompts: Ask for short but effective reasoning instead of lengthy explanations.
• Track token usage: Keep an eye on how many tokens CoT uses vs. the final answer.
• Choose the right model: For simpler questions, consider using deepseek-chat instead, which is cheaper. No CoT in this case, though.
• Use caching: If asking similar questions repeatedly, caching can reduce input token costs.

Example: Unoptimized prompt

To illustrate how Chain-of-Thought (CoT) output works in DeepSeek-R1 and its impact on pricing, let's consider an example:

from openai import OpenAI

client = OpenAI(
    api_key="<Your_DeepSeek_API_Key>",
    base_url="https://api.deepseek.com"
)

def generate_response(prompt):
    response = client.chat.completions.create(
        model="deepseek-reasoner",
        messages=[
            {"role": "system", "content": "You are a helpful assistant."},
            {"role": "user", "content": prompt}
        ],
        stream=False
    )
    return response.choices[0].message.content

# Example usage
prompt = "Calculate the area of a triangle with a base of 6 cm and a height of 4 cm."
result = generate_response(prompt)
print(result)

CoT:

Okay, so I need to find the area of a triangle with a base of 6 cm and a height of 4 cm. Hmm, let me remember how to do this. I think the formula for the area of a triangle is something like base multiplied by height divided by two. Wait, is that right? Let me think.
When I was in math class, the teacher mentioned that a triangle is basically half of a parallelogram. So if you have a parallelogram, its area is base times height. If you cut it along the diagonal, you get two triangles. That means each triangle would have half the area of the parallelogram. So yes, the formula should be (base × height) / 2. That makes sense. Let me write that down to visualize it better.
Area = (base × height) / 2
Given the base is 6 cm and the height is 4 cm, I can substitute those values into the formula. Let me plug them in step by step.
First, multiply the base and the height: 6 cm × 4 cm. Let me calculate that. 6 times 4 is 24. So that gives me 24 cm². Now, divide that result by 2. So 24 divided by 2 is 12. Therefore, the area should be 12 cm².
Wait, let me verify that. If the base was 6 and the height 4, multiplying them gives the area of the corresponding parallelogram, which would be 24 cm². Then, since the triangle is half of that, dividing by 2 gives 12 cm². Yes, that seems correct.
Is there another way to check this? Maybe using a different method? Let's see. For a triangle, the area can also be calculated using Heron's formula, but that requires knowing all three sides. Since I only have the base and height, that might not apply here. Alternatively, if it's a right-angled triangle, the area would be (1/2)*base*height, which is the same formula. But even if it's not a right-angled triangle, the formula still applies because the height is given. The height is the perpendicular distance from the base to the opposite vertex, so regardless of the triangle's type, as long as we know the base and the corresponding height, the formula works.
Let me draw a mental picture. Imagine a triangle where the base is 6 cm. The height is 4 cm, which means if I were to drop a perpendicular line from the top vertex to the base, that line would measure 4 cm. So, even if the triangle is slanted, that vertical height is still 4 cm. Multiplying base and height gives the area of the parallelogram, so dividing by two gives the triangle's area.
Another way to think about it: If I have two identical triangles, I can put them together to form a parallelogram. The area of that parallelogram is base times height, so each triangle is half of that. Therefore, the area of one triangle is 1/2 * base * height.
So, plugging the numbers in again: 1/2 * 6 cm * 4 cm. 1/2 of 6 is 3, and 3 times 4 is 12. Yep, 12 cm².
I think that's solid. Let me check with an example. Suppose the base was 2 cm and the height 3 cm. Then the area would be (2*3)/2 = 3 cm². If I draw such a triangle, it should have an area of 3 cm², which seems right. So scaling up, with a base of 6 and height of 4, the area is proportionally larger.
Alternatively, if I consider a rectangle with the same base and height, area would be 6*4=24 cm². The triangle is half of that, so 12 cm². That also checks out.
Wait, but hold on. If the triangle isn't a right triangle, does the formula still hold? Let's think. If I have an obtuse triangle where the height is outside the triangle, does that affect the area? For example, suppose the base is 6 cm, but the height is measured from the base to a vertex that's outside the triangle, making an obtuse triangle. Even in that case, the area is still (base*height)/2. Because the height is the perpendicular distance regardless of where it's located. So even if the triangle is obtuse, the formula remains the same. Therefore, regardless of the triangle type, as long as the height is given, the formula applies.
Therefore, using 6 cm and 4 cm, multiplying them, dividing by two, gives 12 cm². That seems to be the correct answer. I can't see any mistakes in the reasoning.
Let me just recap. The formula for the area of a triangle is 1/2 multiplied by base multiplied by height. Given base = 6 cm, height = 4 cm. Plugging into the formula: 1/2 * 6 * 4 = 12. The units are in centimeters, and since area is in square units, the answer is 12 cm².
Yes, that all lines up. I think I've got it right. The area is 12 square centimeters.

Final answer:

The area of the triangle is 12 cm².
To calculate the area of a triangle with a base of 6 cm and a height of 4 cm, we use the standard formula:
Area=1/2×base×height
Step-by-Step Calculation
Multiply the base and height: 6 cm×4 cm=24 cm²Divide the result by 2: 24 cm²/ 2=12 cm²Final Answer: 12 cm²
Thus, the area of the triangle is 12 cm².

Cost calculation

• Tokens Used = 1165 approximately
• Cost Per Million Tokens = $2.19
• Convert tokens to millions: 1165 tokens÷1,000,000=0.001165 million tokens
• Multiply by cost per million tokens: 0.001165×2.19=0.002551350.
• Final Cost ≈ $0.00255 (rounded to five decimal places)

Example: Optimized prompt

Now, let’s refine the prompt and see how the output changes:

Prompt: "Area of triangle: base 6cm, height 4cm. Show formula and result only"

CoT:

Okay, so I need to find the area of a triangle with a base of 6 cm and a height of 4 cm. Hmm, let me remember the formula for the area of a triangle. I think it's something like base multiplied by height divided by two. Wait, yeah, right, because a triangle is basically half of a parallelogram, right? So if you have a parallelogram, the area is base times height, and then a triangle would be half of that. So the formula should be (base * height) / 2.
Let me double-check that. Maybe I can visualize a triangle with base 6 and height 4. If I had another identical triangle, I could put them together to form a parallelogram. The base would still be 6, the height would still be 4, so the area of the parallelogram would be 6*4=24. Then the area of one triangle would be half of that, which is 12. So that makes sense.
Alternatively, I remember in school they taught us the formula as A = 1/2 * b * h. So plugging in the values, it should be 1/2 * 6 cm * 4 cm. Let me calculate that. 1/2 of 6 is 3, then 3 times 4 is 12. So the area should be 12 cm².
Wait, but just to be thorough, let me make sure there aren't any other formulas that could apply here. For example, Heron's formula requires the lengths of all three sides, but I only have the base and height here. So Heron's formula isn't necessary. Since we have the base and height given directly, using the standard area formula is the way to go.
Also, units: the base is in centimeters, the height is in centimeters, so when multiplying, the area will be in square centimeters. That checks out.
Another thing to consider: is the height corresponding to the given base? The problem states "base 6 cm, height 4 cm," so yes, they correspond. If the height was relative to a different side, it might complicate things, but here it's specified for the base. So no issues there.
I think that's all. The formula is correct, the calculation seems right. 6 times 4 is 24, divided by 2 is 12. So the area is 12 square centimeters. 

Final answer:

The area of the triangle is calculated using the formula: Area=1/2×base×height
Substituting the given values: Area=1/2×6 cm ×4 cm = 12 cm²
Result: 12 cm²

Cost calculation

• Tokens Used = 496 approximately
• Cost Per Million Tokens = $2.19
• Convert tokens to millions: 496 tokens÷1,000,000=0.000496 million tokens
• Multiply by cost per million tokens: 0.000496×2.19=0.001086240.
• Final Cost ≈ $0.00109 (rounded to five decimal places)

Final Cost Comparison Table

The table below shows how the number of tokens used affects the total cost of an API call:

Example	Tokens Used	Cost (USD)
Unoptimized Prompt	1165	$0.00255
Optimized prompt	496	$0.00109

We reduced costs by about 57% compared to the original with the optimized prompt, while still getting the correct answer.

How to Use DeepSeek’s Context Caching to Cut Costs

From the table on pricing that we’ve seen in the Token Costs section, we can conclude that caching saves us about 74.07% in API costs for deepseek-chat and 74.55% for deepseek-reasoner when compared to the cost of processing new (uncached) input tokens. This means that using caching effectively can reduce input token costs by nearly three-quarters.

It is especially useful for long prompts, as it reduces waiting time. Plus, the system automatically handles caching—no need to change your code.

But how does context caching work?

When you send a request, DeepSeek stores the input on its servers. If you send a similar request later, the system retrieves the stored response instead of recalculating everything. This makes the process faster and cheaper.

When is caching most useful?

Caching can be useful and reduce costs in the following situations:

• Multi-turn conversations: Chatbots can reuse previous responses, which would reduce costs.
• Data analysis: Repeated queries on the same files benefit from cached responses.
• Q&A assistants: Long instructions at the start of conversations can be cached.
• Role-playing & interactive apps: Character settings and long dialogues don’t need to be recalculated.
• Code analysis: Referencing the same code files multiple times saves tokens.
• Few-shot learning: If you're feeding examples to the model, caching can cut costs.

How to maximize cost savings

To maximize cost savings, this is what I’d recommend:

• Keep reused text at the beginning: The API only caches the start of inputs.
• Use similar inputs: Avoid changing prompts too much if you want to hit the cache.
• Design for Repetition: Structure your requests to reuse as much cached content as possible.

How to track your cache usage

To track your cache usage with DeepSeek's API, you don't need to modify your code. The cache usage information is automatically included in the API response. The caching system is enabled by default for all users. When you make an API call, the response object will include two new fields in the usage section:

• prompt_cache_hit_tokens: Number of input tokens served from the cache
• prompt_cache_miss_tokens: Number of input tokens not found in the cache

To access this information, you need to check the usage field in the API response. Here's an example of how you can access these values in:

response = client.chat.completions.create(
    model="deepseek-chat",
    messages=[
        {"role": "user", "content": "You are a helpful assistant."}
    ]
)

cache_hits = response.usage.prompt_cache_hit_tokens
cache_misses = response.usage.prompt_cache_miss_tokens

print(f"Cache hits: {cache_hits}")
print(f"Cache misses: {cache_misses}")Powered By 

This feature allows you to monitor how the caching system works for your use case. 

Caching has some limitations, though:

• Minimum cache size: The system only caches text chunks of 64 tokens or more. Shorter inputs won't be stored.
• Not 100% reliable: The system doesn’t guarantee every request will hit the cache.
• Cache expires over time: If unused, cached content automatically clears within a few hours to days.

Conclusion

In this tutorial, we have learned how to use DeepSeek API and its two models, DeepSeek-R1 and V3. If you understand how these models work, you can build smart, cost-efficient AI applications.

Keep an eye on the latest DeepSeek documentation and best practices to make the most of these powerful models.

Happy coding!

Reposted from: DeepSeek API: A Guide With Examples and Cost Calculations | DataCamp